中，共有6个案例被评为2017年度优秀会计案例并纳入我市优秀会计案例库为发挥优秀会计案例引领示范作用，促进我市各单位会计工作上水平，我会将以微信形式对优秀会计案例开展系列宣传。

  目前，ABC电力销售有限公司（以下简称“ABC公司”）已不断的提高预算及存量资金管理上的水准，但在制定安全备付额度方面仍缺乏科学的预测模型等数据支撑工具。本次工作主要是通过对最佳现金持有量在科学性预测方面的逐渐完备，最大限度减少资金闲置，提高资金的使用效率。

  本次研究主要是通过对现金科目日记账以及凭证信息等数据来进行关联及清洗，从而获取每一日ABC公司的净现金流，以预测2017年的长中短期的最佳现金持有量。此研究工作主要从三个方面展开：一是对2014-2017年每日净现金流数据来进行清洗及观测。二是对已有现金持有量预测模型做评估。三是利用科学性预测模型对现金流进行预测。

  随着电网企业的盈利能力及发展能力的慢慢地加强，在保障生产经营及建设资金的情况下，充分的利用闲置资金实现效益最大化，提高对等高风险情况的整体调控力。

  本次研究主要是通过对现金科目日记账以及凭证信息等数据来进行关联及清洗，从而获取每一日ABC公司的净现金流，以预测2017年的长中短期的最佳现金持有量。

  从数据对象范围看，本次研究的研究对象范围为ABC公司及其子公司（D公司、E公司）；数据时间范围为2014年1月1日至2017年5月8日。数据内容最重要的包含现金日记账、凭证信息以及E公司凭证信息三类。

  从数据质量看，ABC公司及其子公司在2014年1月到2017年5月共有38.9万条凭证信息，关联后只保留两者相交部分的凭证信息，共38.6万条。

  根据现金收入及现金支出凭证信息，发现ABC公司的收入来源较单一而支出渠道较为多样化。

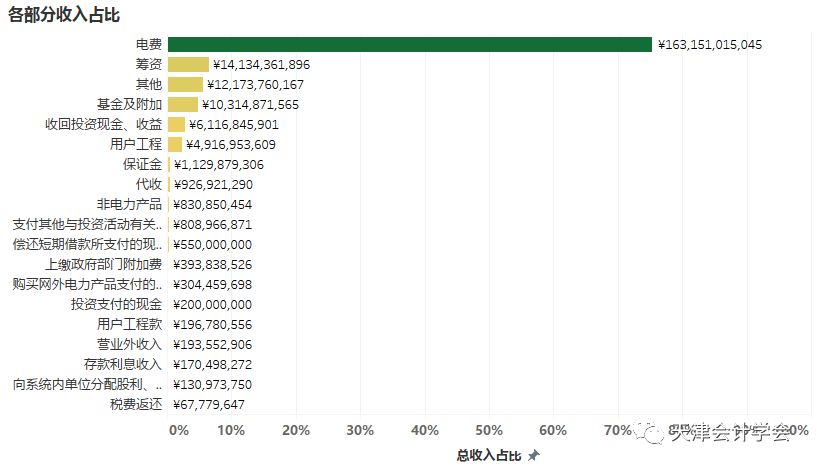
  根据日期，将每日的收入和支出汇总，发现收入和支出都存在较强的周期性，一般在月末易发生较大金额的收支。初步考虑将金额较大且日期固定的发生额提取出，对其余现金流采用随机过程进行拟合。

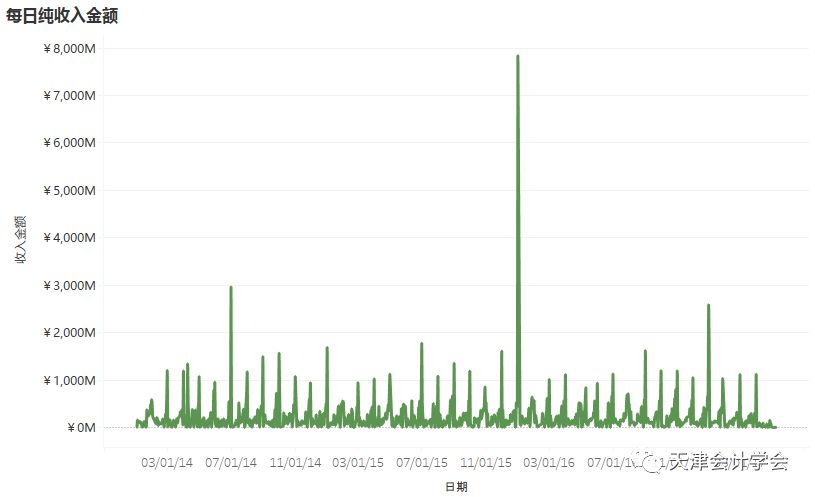
  根据日期，将2014年1月至2017年4月每日售电收入及购电支出的金额汇总，发现售电日期大多分布在在月底（30号及31号），而购电日期分布未呈现一定规律，因此无法将金额较大且日期固定的发生额提取出，应考虑对净现金流整体进行预测。

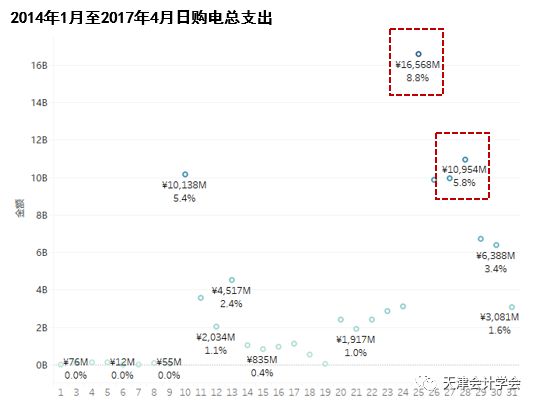
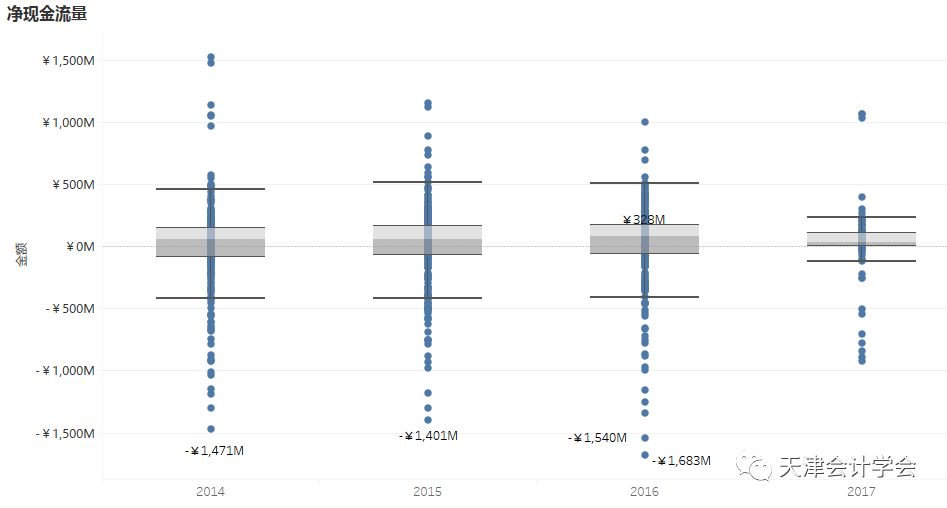
  根据日期获取每日净现金流量（每日收入减去每日支出）探索净现金流随时间的变动情况，可发现除2016年1月1日外，净现金流在正负20亿之间浮动。考虑现金流服从一定的统计分布，可根据其统计性质预测现金流的波动情况。

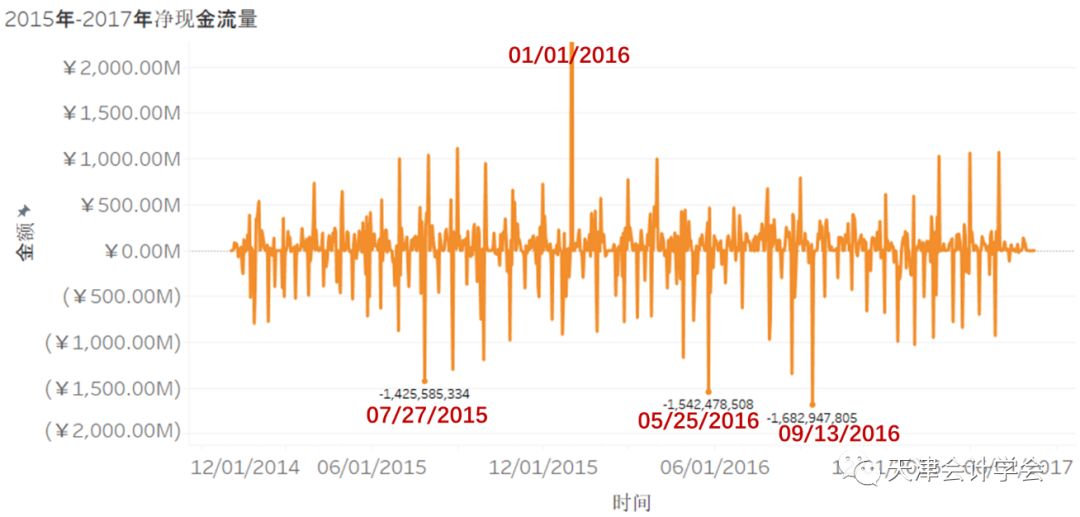
  将2014年到2017年每日的净现金流量用箱线图展示，可发现前三年净现金流量的分布较为相似。若取最小负现金流作为安全备付额度（即保证全年不出现金额短缺现象），则2016年每日需维持备付金额17亿，2014年及2015年每日只需维持备付金额15亿。

  成本分析模型指通过一系列分析持有现金的成本，寻找持有成本最低点对应的现金持有量。其中将企业持有现金造成的成本分为三类：机会成本、管理成本和短缺成本，三项成本之和最小的现金持有量，便为最佳现金持有量。

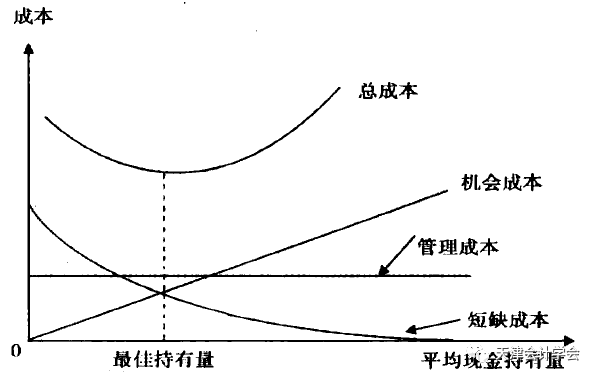
  结合真实的情况来看，ABC公司的机会成本较小，且短缺成本难以估计，故总成本的估计难以确定。因此，用成本分析模型来确定最佳持有量并不可取。

  存货模型指若企业平时只持有少量现金，在这一模型中，将企业拥有现金造成的成本分为机会成本及交易成本，其中交易成本主要指将有价证券转换为现金的成本。

  使用该模型时，需要假设现金总量稳定并可预测，整个期间内现金收支均匀分布，波动少；ABC公司所面临的机会成本较少，当前模式并不支持现金与有价证券之间的转换。

  由于电网公司无法灵活的将现金与有价证券进行转换，且现金余额变化的标准差相对固定，导致该模型计算出的持有量相对保守，无法很好预测最佳现金持有量。

  综上分析，上述三种常见的现金持有量预测模型，在应对复杂的现实情况下差强人意。因此，需要结合ABC公司业务特点、现金收入和支出特性选择更加实用的预测工具建立最佳资金持有量预测模型。

  蒙特卡洛模拟法（简称MC）主要依据市场数据估计历史波动参数，模拟出市场因子未来波动的大量可能路径。

  风险价值模型（Value at Risk）指给定置信区间的一个持有期内的最坏预期损失。例如，在给定持有期为一个星期，给定置信水平为99%的条件下，某资产组合的VaR为1000万人民币。则在下一个星期内99%的概率下，该资产组合的最大损失不会超过1000万人民币，即有1%的概率在下一星期内损失超过1000万人民币。VaR的计算公式如下：

  蒙特卡洛模拟法计算风险价值假设期货的价格变革服从某种随机过程的形态，可用计算机来仿真，产生若干次可能价格的路径，并以此构建期货的报酬分配，进而估计其风险值。选择价格随机过程，最常用的模型是几何布朗运动，即随机行走模型，其离散形式可表示为：

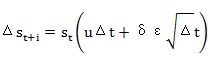
  将一天的持有期分为20个时间段（小时）， 为开始时间的期货价格， 为 t+i 时刻的期货价格， 表示每个时间段内期货价格的变化量。若每个时间段内期货价格的均值和标准差分别为 和 ， t+i 时刻的期货价格为：

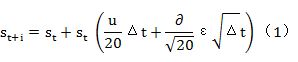
  使用历史数据计算22个交易日的收盘价的日收益率的均值和方差，并计算每个时间段内的期货价格日收益均值和方差（ 和 ）；

  根据确定的置信水平，计算风险价值水平。如置信水平为5%时，寻找直方图（ 排列）的下方5%分位数 ，则在95%的置信水平下的风险价值为 与 的差值；

  循环神经网络是一种计算机制，即由简单函数串联起来的复杂函数，能学习长期依赖信息。

  循环神经网络结构如图所示。 不同于普通神经网络，循环神经网络引入了定向循环，可处理那些输入之间前后关联的问题。

  通过Python软件将负现金流与79个已知分布进行拟合，发现负现金流量服从（alpha = 3.06， beta = 0.49）的Beta分布，且拟合程度较高。

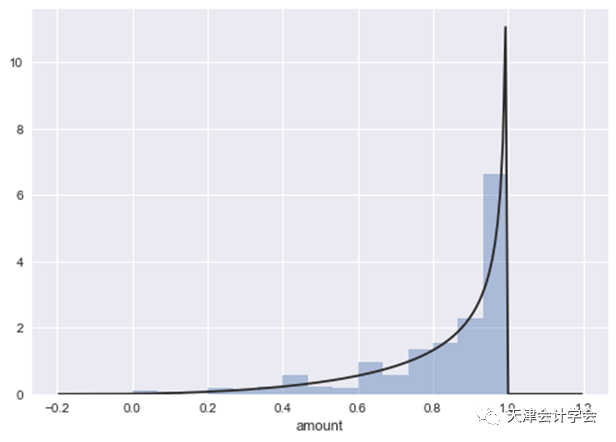
  在统计学判定样本是否服从已知分布时，先假定样本服从已知分布，并计算此时的检测值，并将检测值与查询到的统计值相比对，判定是否拒绝原假设。

  通过上一步的分析，得知负现金流量服从（alpha = 3.06， beta = 0.49）的Beta分布。本部分通过对该分布进行100万次的蒙特卡洛模拟，获取模拟金额的分布，求取风险价值，这样做才能够增加样本点数，提高模拟稳定性。

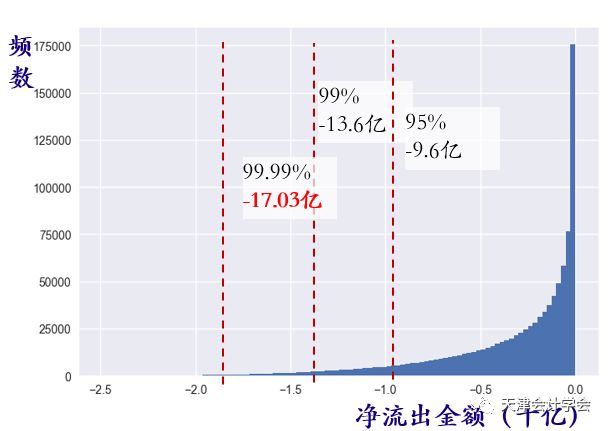
  通过上一步的得到蒙特卡洛模拟的净流出的金额分布，设定风险水平为0.1%，获取安全备付额度的预测值为17.03亿，即未来在99.9%的概率下，一日的净流出不会超过17.03亿，全年维持这一水平即可。

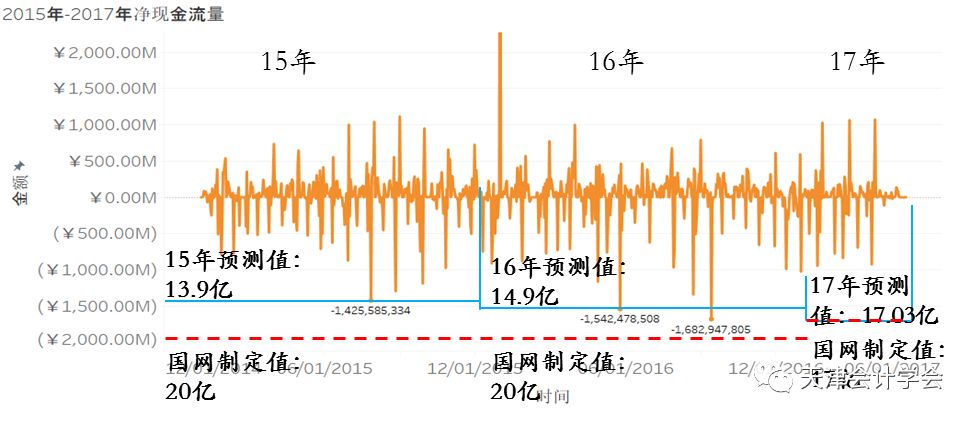
  通过上述方法，可通过2014年支出现金流量计算2015年最佳现金持有量，利用2014-2015年支出现金流量计算2016年最佳现金持有量，计算的最佳现金持有量与实际支出现金流量如图所示。计算的15年、16年与17年的最佳现金持有量分别为13.9亿、14.9亿以及17.07亿。从2015年1月至2017年4月期间，只有3天超出了计算最佳现金持有量。2015年与2016国网定制备付金额均为20亿，2017年国网定制金额为17亿。

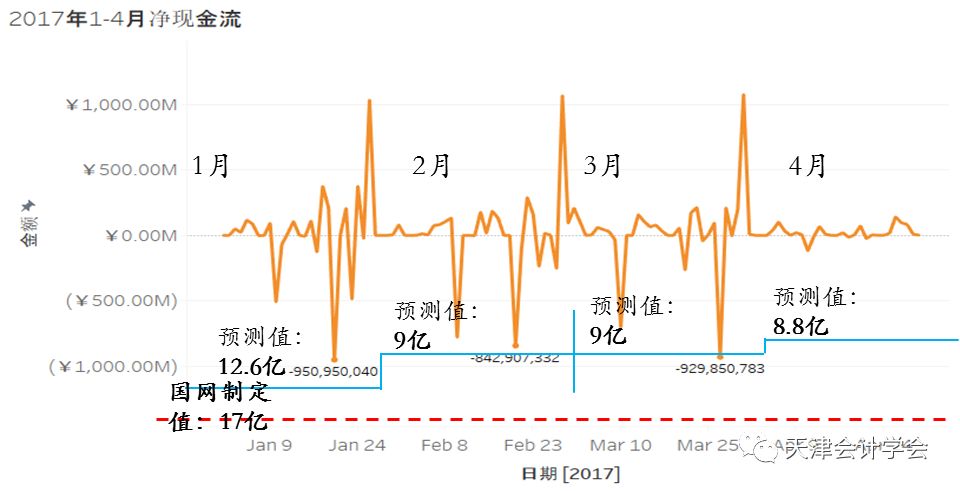
  利用相同的方法，将14-16年的现金流以月份为依据分为12份，对每一份进行蒙特卡洛模拟及风险价值测算，获取未来每月（中期）最佳备付额度预测值。

  1月至4月间实际现金支出均为超出计算值。预测支出金额最多的天所在月份为9月份，金额为16.8亿，未超出预测的17.03亿。

  将中长期模型应用于E公司与D公司， 计算得出E公司2017年1-4月最佳现金持有量分别为：1.07亿，3.24千万，1.17千万以及1.87千万，前四月支出没有超出预测值。E公司年度预测最佳现金持有量为8200万。

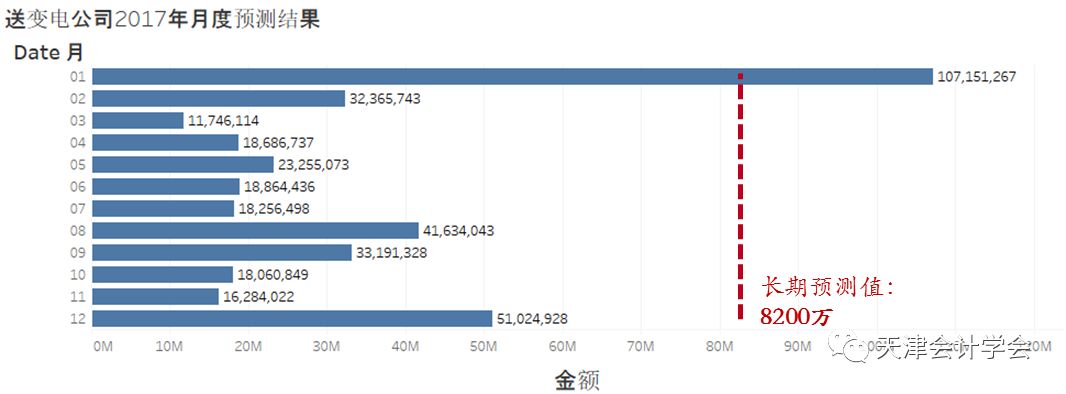
  计算得出D公司2017年1-4月最佳现金持有量分别为3.23亿、2.05亿、3.20亿以及3.36亿。2017年1月至4月中有2天超出预测值。其中2月27日超出预测值5.6%，3月30日超出预测值0.6%。D公司年度最佳现金持有量为7.44亿。月度预测值均小于年度预测值 。

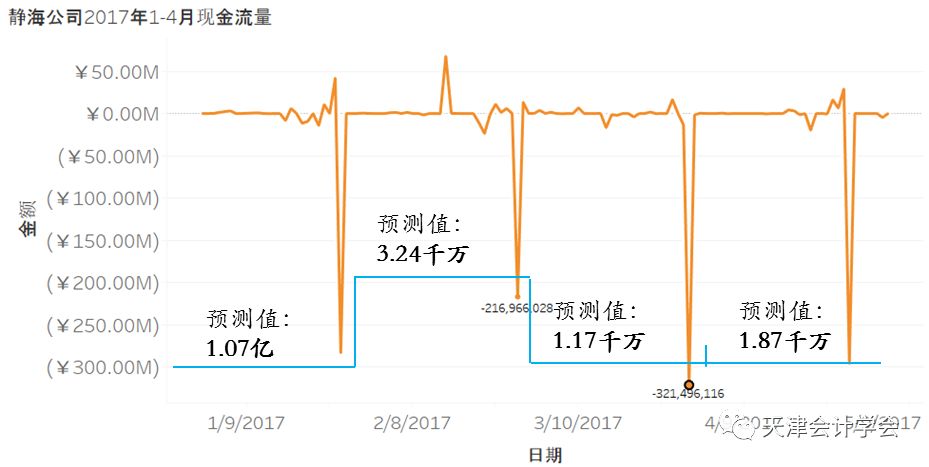
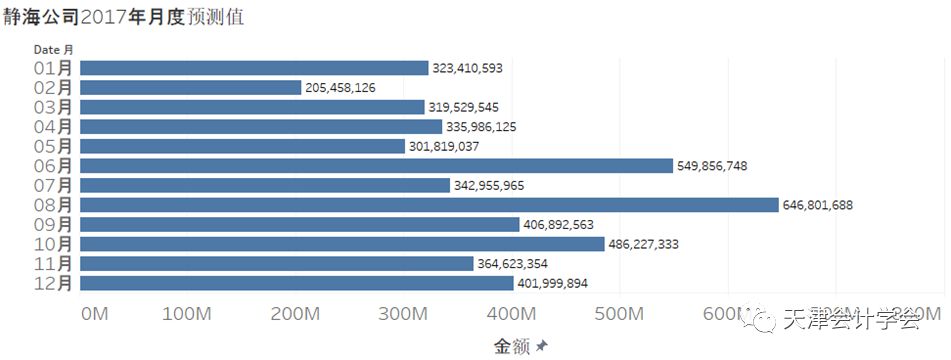
  当有效条目少于60条时，会影响预测精度。同时当条目较少，也会影响分布拟合。

  主要步骤为数据筛选、数据预处理、模型训练与调参、误差获取、最优模型选择、日现金流预测。

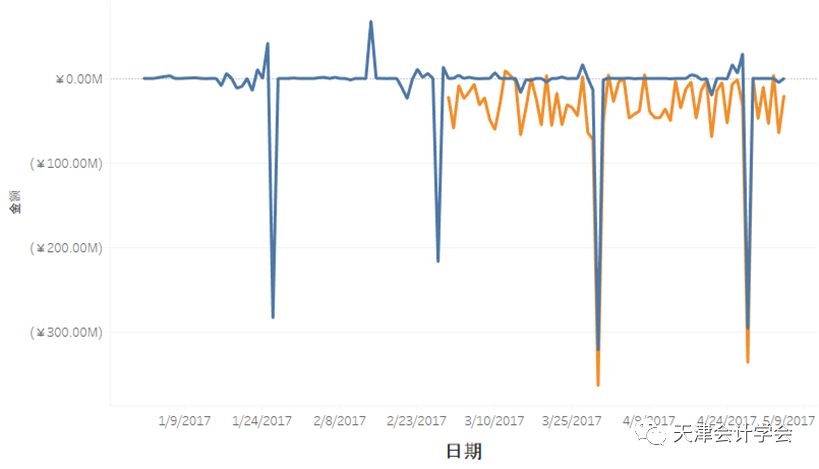
  对于支出渠道来说，最重要的包含购电、工程支出、政府部门附加费及税费四类支出。

  2014年1月1日2017年4月30日，除2016年1月1日外，净现金流在正负20亿之间浮动。

  通过统计验证，发现2017年以前的净流出服从（ alpha=3.47 ，beta=0.54）的beta分布。基于该结论，建立了基于统计的年度和月度最佳现金持有量模型，能够适用于预测年度和月度最佳现金持有量。

  利用长短期记忆循环神经网络计算方式可以实现日现金流量预测。其中最好的模型为将8天分为一组，即利用前19天的现金流量预测第20天的现金流量。

  通过中长期以及日现金流量的预测，能提高现金预算及存量资金精益化管理上的水准，为制定安全备付额度提供科学性预测模型等数据支撑工具。